VASP计算材料的弹性矩阵和杨氏模量

一、从1D到3D材料的胡克定律(Hooke’s law)

1.1D材料的胡克定律

1D材料的胡克定律也就是我们所熟知的线弹性模型，即是我们初中阶段就学习过的$F=k\Delta{x}$，用更加标准和统一的形式可以写作：

$\sigma = C\epsilon$

对于1D材料，其中三个关键参数分别为：

• $\sigma$：应力，标量，SI制下的单位为$N$
• $C$：弹性常数，标量，SI制下的单位为$N$
• $\epsilon$：应变，标量，表达式为 $\frac{l-l_0}{l_0}=\frac{\Delta{l}}{l_0}$
  值得注意的是，考虑到在变形过程中材料的弹性常数并不是恒定的，因此在这里计算应力和应变有两种方法并且通常存在一定差别，这就是我们常说的工程应力、工程应变和真应力、真应变，具体可以参考这篇帖子：https://www.zhihu.com/question/294496637

2.2D材料的胡克定律

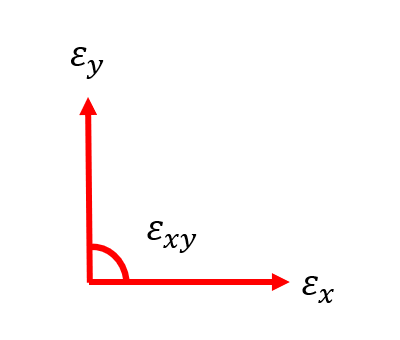
相较于1D材料，2D材料除了增加了一个维度的正应变之外，还多出了一个切应变，如下图所示：

相应地应力部分多出了一个切应力，用公式表示为：

$\begin{pmatrix} \sigma_{xx} \\ \sigma_{yy} \\ \sigma_{xy} \\ \end{pmatrix} = \begin{pmatrix} C_{11}&C_{12}&C_{13} \\ C_{21}&C_{22}&C_{23} \\ C_{31}&C_{32}&C_{33} \\ \end{pmatrix} \begin{pmatrix} \epsilon_{xx} \\ \epsilon_{yy} \\ \epsilon_{xy} \\ \end{pmatrix}$

其中应力的表达式为：

$\sigma = \frac{F}{l}$

对于正应力，$l$是指与力垂直方向的长度，对于切应力，$l$是指与力平行方向的长度，正应变的定义与1D的情况是一致的，而切应变指的是角度的变化，即是：$\epsilon_{xy}=\frac{\theta-\theta_0}{\theta_0}=\frac{\Delta{\theta}}{\theta_0}$，应力和弹性矩阵在SI制下的单位都是$N/m$，而应变同样是无量纲的数。

3.3D材料的胡克定律

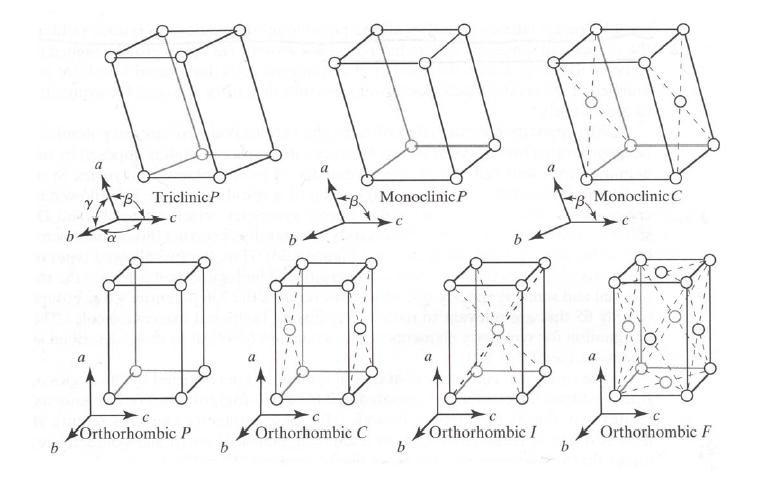
类似地，3D材料的胡克定律与上面具有相似的形式，不同的是由于维度的增加导致材料的变形自由度增加，如下图所示：

相应的表达式变为：

$\begin{pmatrix} \sigma_{xx} \\ \sigma_{yy} \\ \sigma_{zz} \\ \sigma_{xy} \\ \sigma_{xz} \\ \sigma_{yz} \\ \end{pmatrix} = \begin{pmatrix} C_{11}&C_{12}&C_{13}&C_{14}&C_{15}&C_{16} \\ C_{21}&C_{22}&C_{23}&C_{24}&C_{25}&C_{26} \\ C_{31}&C_{32}&C_{33}&C_{34}&C_{35}&C_{36} \\ C_{41}&C_{42}&C_{43}&C_{44}&C_{45}&C_{46} \\ C_{51}&C_{52}&C_{53}&C_{54}&C_{55}&C_{56} \\ C_{61}&C_{62}&C_{63}&C_{64}&C_{65}&C_{66} \\ \end{pmatrix} \begin{pmatrix} \epsilon_{xx} \\ \epsilon_{yy} \\ \epsilon_{zz} \\ \epsilon_{xy} \\ \epsilon_{xz} \\ \epsilon_{yz} \\ \end{pmatrix}$

其中应力的表达式为：

$\sigma = \frac{F}{S}$

同样地，对于正应力，$S$为垂直于力方向平面的面积，对于切应力，$S$为平行于力方向平面的面积，应变的定义与2D情况是相同的，其中$\epsilon_{xy}$、$\epsilon_{xz}$和$\epsilon_{yz}$分别对应上图中角度$\alpha$、$\beta$和$\gamma$的变化。

二、对称性和弹性矩阵

由于结构本身固有的平移和旋转对称性，因此弹性矩阵是对称矩阵，对于2D材料，独立的矩阵元变为6个，对于3D材料，独立的矩阵元变为21个。

1.2D材料的对称性和弹性矩阵的关系

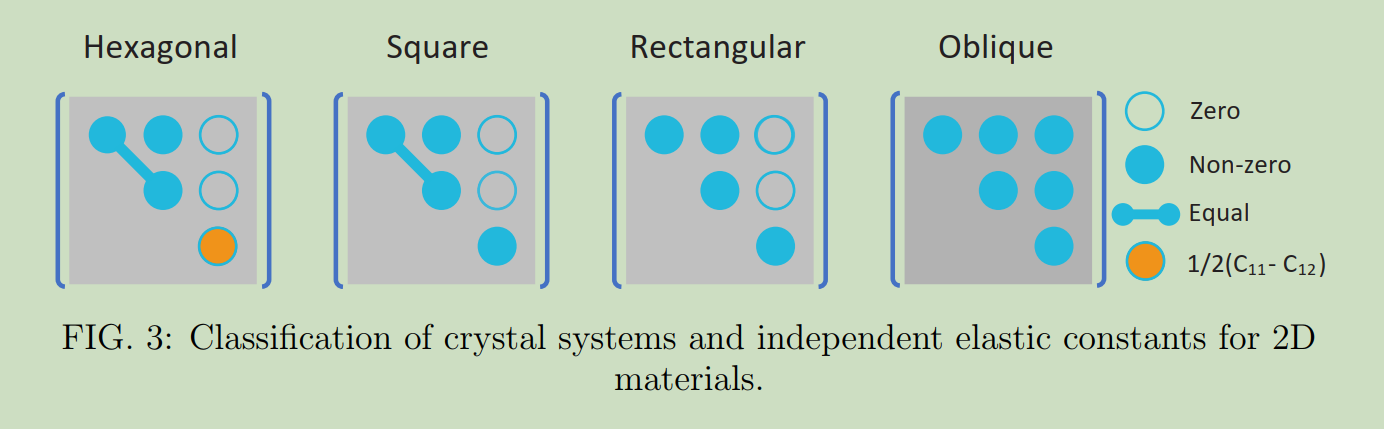
2D材料的晶格主要有六角形、正方行、长方形和普通倾斜形，它们所对应的弹性矩阵形式分别如下图所示：

2.3D材料的对称性和弹性矩阵的关系

3D材料的晶格一共有7种，即7大晶系，其中三斜晶系材料弹性矩阵中独立的矩阵元有21个，单斜晶系有15个，正交晶系有9个，三方晶系有7个，四方晶系有5个，六方晶系有5个，立方晶系有3个，具体形式可以参考这篇文章：
https://zhuanlan.zhihu.com/p/387677721

3.材料的柔度矩阵

在$\sigma=C\epsilon$关系中，我们在等式左右都乘以C的逆矩阵，即得到：

$\epsilon = C^{-1}\sigma=S\sigma$

这里我们就得到了材料的柔度矩阵$S$，它是材料弹性矩阵的逆矩阵，这里要注意两个表达式的因果关系，弹性矩阵反映的是材料变形所产生的应力大小，而柔度矩阵反映的是施加应力之后材料的变形大小。

三、材料的各向异性杨氏模量和泊松比

1.杨氏模量和泊松比

• 杨氏模量：在物体的弹性限度内，应力与应变成正比，这一比值就被称为材料的杨氏模量，对于1D情况，杨氏模量等于材料的弹性常数，对于2D情况，杨氏模量和面内$\theta$角有关，对于3D情况，杨氏模量和球坐标系中材料的方位角有关。
• 泊松比：泊松比的定义为材料在发生形变时，材料横向应变和纵向应变的比值。对于2D和3D材料，泊松比同样存在各向异性的情况。

2.3D材料的杨氏模量和泊松比

3D材料的具体推导过程较为复杂，具体参考这篇文献：https://www.sciencedirect.com/science/article/pii/S0010465521003076，这里只大致说一下结论。

杨氏模量

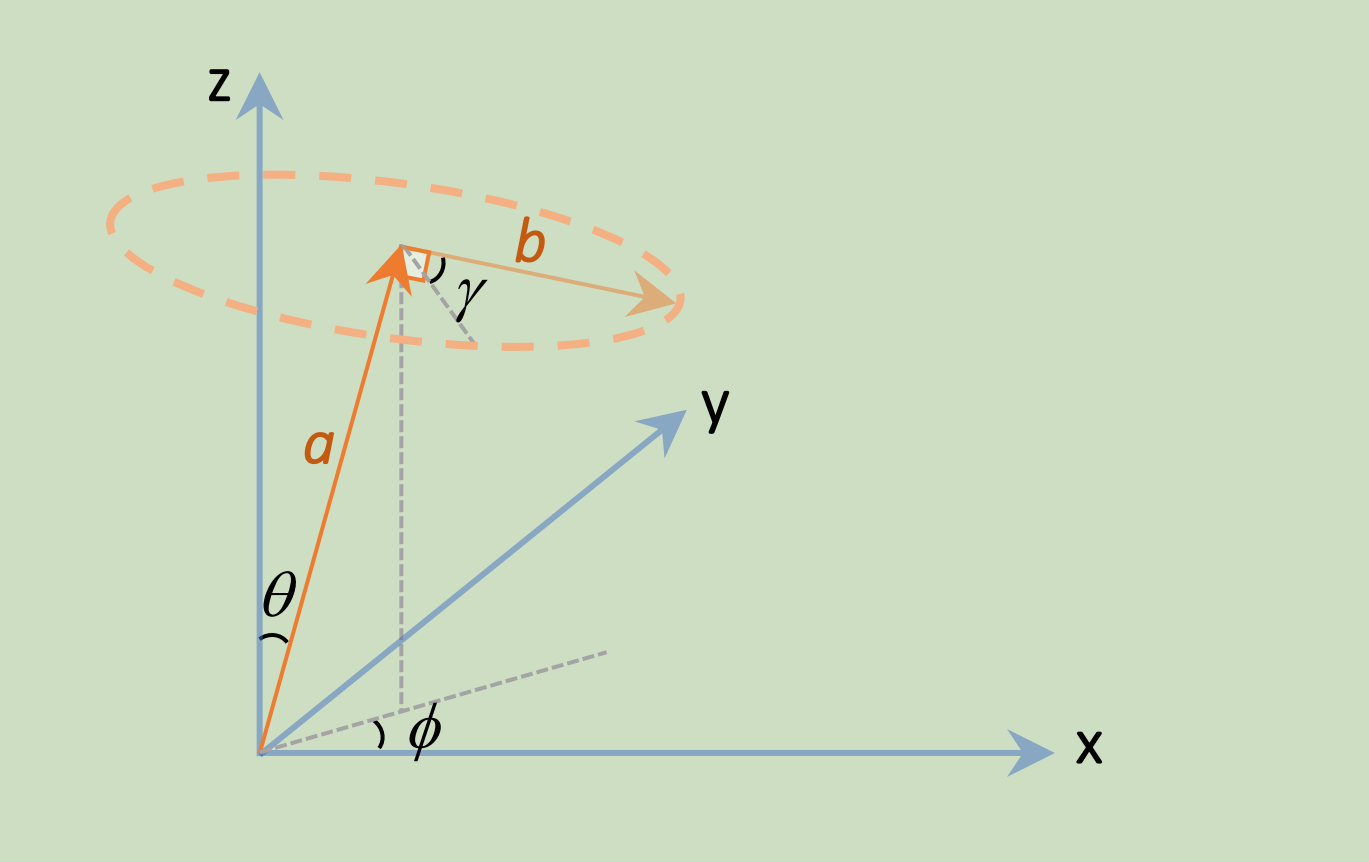
在3D空间中，如下图所示：

我们首先在球坐标系中确定我们的自变量，即单位矢量：

$\vec{a} = \begin{pmatrix} sin(\theta)cos(\varphi) \\ sin(\theta)sin(\varphi) \\ cos(\theta) \end{pmatrix} ; 0\leq\theta \leq \pi , 0 \leq \varphi \leq \pi.$

以该变量为自变量，我们就能求出空间中任意一点的杨氏模量，具体表达式为：

$\frac{1}{E(\vec{a})} = \sum _{i,j,k,l=x,y,z} a_i a_j a_k a_l S_{ijkl}$

其中S为材料的柔度矩阵。

需要注意的是这里计算我们使用的是 3x3x3x3 四维柔度矩阵，而传统计算得到的是 6x6 的二维矩阵，要用上面的公式计算杨氏模量需要把二维柔度矩阵转换成四维柔度矩阵，转换使用 Voigt 方案，具体参考这篇文献：https://www.sciencedirect.com/science/article/abs/pii/S0010465521003076,用表格可以写作：

$\begin{array}{cc} lattice & xx & yy & zz & yz & xz & xy \\ S_{(ij)(kl)} & 11 & 22 & 33 & 23,32 & 31,13 & 12,21 \\ S_{(m)(n)} & 1 & 2 & 3 & 4 & 5 & 6 \\ \end{array}$

并且需满足：

$S_{ijkl} = S_{mn},i=j \And k=l \\ S_{ijkl} = \frac{S_{mn}}{4},i \neq j \And k\neq l \\ S_{ijkl} = \frac{S_{mn}}{2},i \neq j \quad or \quad k\neq l$

泊松比

对于3D材料的泊松比，我们还需要定义一个垂直于$\vec{a}$的单位矢量$\vec{b}$,如上图中所示，与$\vec{a}$垂直的矢量分布在一个锥面的底面上，不唯一，因此这里还要引入一个额外的自由度$\gamma$，$\vec{b}$的表达式为：

$\vec{b} = \begin{pmatrix} cos(\theta)cos(\varphi)cos(\gamma)-sin(\theta)sin(\gamma) \\ cos(\theta)sin(\varphi)cos(\gamma)-cos(\theta)sin(\gamma) \\ -sin(\theta)cos(\gamma) \end{pmatrix} ; 0\leq\gamma \leq 2\pi.$

相应地泊松比的表达式为：

$\upsilon(\vec{a}, \vec{b})=-\frac{\sum_{i,j,k,l=x,y,z}a_ia_jb_kb_lS_{ijkl}}{\sum _{i,j,k,l=x,y,z} a_i a_j a_k a_l S_{ijkl}}=-E(\vec{a})\sum_{i,j,k,l=x,y,z}a_ia_jb_kb_lS_{ijkl}$

3.2D材料的杨氏模量

对于2D材料，杨氏模量和泊松比都具有角度依赖性，不同的是，二维材料的杨氏模量和泊松比仅和xy面内的$\varphi$有关，因此这里我们定义的自变量的形式如下：

$\vec{a}= \begin{pmatrix} cos(\varphi) \\ sin(\varphi) \\ 0 \end{pmatrix}; \vec{b} = \begin{pmatrix} -sin(\varphi) \\ cos(\varphi) \\ 0 \end{pmatrix}; 0\leq \varphi \leq 2\pi.$

2D材料的杨氏模量和泊松比表达式和3D材料应该具有相同的形式，不同的是，2D材料缺少了z方向的维度，相应的表达式为：

$\frac{1}{E(\vec{a})} = \sum _{i,j,k,l=x,y} a_i a_j a_k a_l S_{ijkl} \\ \upsilon(\vec{a}, \vec{b})=-E(\vec{a})\sum_{i,j,k,l=x,y}a_ia_jb_kb_lS_{ijkl}$

与3D材料类似，要使用上式计算，需要将二维 3x3 的柔度矩阵转换成四维 2x2x2x2 的柔度矩阵，具体转换方法可以参考3D材料的方法。

当然由于2D材料相对3D材料表达式得到了简化，所以我们也可以直接推导出3D材料的角度依赖的杨氏模量和泊松比的具体形式：

$\frac{1}{E(\varphi)}=S_{11}cos^4(\varphi) + S_{22}sin^4(\varphi) + (S_{33}+2S_{12})cos^2(\varphi)sin^2(\varphi)+ \\ 2S_{13}cos^3(\varphi)sin(\varphi) + 2S_{23}cos(\varphi)sin^3(\varphi)$

$\upsilon(\varphi)=-E(\varphi)*\Bigg \lbrack \\ \bigg ( S_{11}sin^2(\varphi)+S_{12}cos^2(\varphi)-S_{13}sin(\varphi)cos(\varphi) \bigg )cos^2(\varphi) +\\ \bigg ( S_{21}sin^2(\varphi)+S_{22}cos^2(\varphi)-S_{23}sin(\varphi)cos(\varphi) \bigg )sin^2(\varphi) +\\ \bigg ( S_{31}sin^2(\varphi)+S_{32}cos^2(\varphi)-S_{33}sin(\varphi)cos(\varphi) \bigg )cos(\varphi)sin(\varphi) +\\ \Bigg \rbrack \\ =-E(\varphi)*\Bigg \lbrack \\ \bigg ( S_{11}+S_{22}-S_{33} \bigg )cos^2(\varphi)sin^2(\varphi) +\\ S_{12} \bigg ( cos^4(\varphi) + sin^4(\varphi) \bigg) +\\ \bigg ( S_{13}-S_{23} \bigg ) ( cos(\varphi)sin^3(\varphi) - cos^3(\varphi)sin(\varphi) \bigg )\\ \Bigg \rbrack$

四、用vasp计算材料的弹性矩阵

用vasp计算材料的弹性常数主要分为以下三步：

1.充分弛豫初始结构

对于3D材料，结构弛豫较为简单，这里不再多说。对于2D材料，结构弛豫稍微复杂，首先需要建立slab结构，然后在弛豫的过程中需要保持晶胞c轴固定，这里有两种方法，一种是使用ISIF=4即体积不变来弛豫结构，第二种是稍微修改vasp代码来实现，具体参考这篇文章：http://bbs.keinsci.com/thread-13114-1-1.html。

2.计算弹性常数

这步需要修改相应的参数，主要是：

• IBRION = 6
• ISIF = 3
• NFREE = 4 #四阶插值
• NSW = 1

为了加快计算速度，建议打开对称性，即 ISYM = 2。

3.提取弹性矩阵

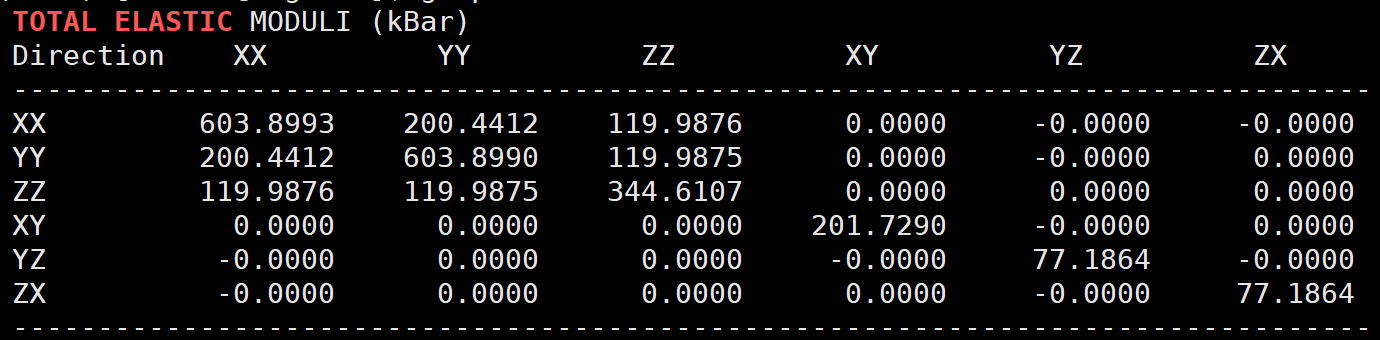
计算完成后，直接用命令 grep -A 9 “TOTAL ELASTIC” OUTCAR 就能得到材料的弹性矩阵，如下图所示：

单位为kBar，单位换算关系为：

$1kBar = 0.1GPa = 100MPa = 10^8Pa=10^8\frac{N}{m^2}$

对于二维材料，计算应力时我们只需要用力除以长度，不考虑c轴，因此弹性常数的单位为N/m，但是vasp计算时没有考虑这些，因此我们需要将计算结果乘以c轴的长度$l_c$，即是

$C_{2D} = C_{3D}*l_c$

这里需要注意的是c轴长度的单位A，而C的单位是kBar，因此需要转换一下单位，最终结果为$C_{2D}=C_{3D}*0.01*c_z$，得到的弹性矩阵的单位是N/m。

参考资料：https://www.zhihu.com/question/548363029/answer/2701960824

五、杨氏模量和泊松比的计算和画图

后面代码测试所使用的OUTCAR文件来自于JARVIS-DFT数据库中#7974数据，这是链接：https://www.ctcms.nist.gov/~knc6/static/JARVIS-DFT/JVASP-7974.xml，弹性常数数据在 FD-ELAST 文件中，直接下载就可以。

1.Python计算3D材料的空间分布杨氏模量和画图

这里用python直接读取弹性矩阵计算3D材料的空间分布杨氏模量，绘图使用matplotlib库。代码如下：

import numpy as np
import os
import pandas as pd
import matplotlib.pyplot as plt


### 读取弹性矩阵
os.system('grep -A 8 "TOTAL ELASTIC" OUTCAR | tail -6 > ecs.dat')
df_ecs = pd.read_csv('ecs.dat', header=None, index_col=0, delimiter=r"\s+")
dat_ecs = df_ecs.values       ### 得到vasp计算出来的弹性矩阵


### 将vasp给出的弹性矩阵转换成满足Voigt下标的矩阵形式并将单位转换为GPa
dat_c = np.zeros(dat_ecs.shape)
for m in range(6):
    if m <= 2:
        m_ = m
    elif m == 3 or m == 4:
        m_ = m + 1
    elif m == 5:
        m_ = 3
    for n in range(6):
        if n <= 2:
            n_ = n
        elif n == 3 or n == 4:
            n_ = n + 1
        elif n == 5:
            n_ = 3
        dat_c[m, n] = dat_ecs[m_, n_]*0.1
print(dat_c)


### 计算柔度矩阵
dat_s = np.linalg.inv(dat_c)       

### 将二维柔度矩阵转换成四维柔度矩阵
def tranS_ijkl(dat_s):
    '''
    将6x6的二维柔度矩阵转换成3x3x3x3的柔度矩阵
    '''
    S_ijkl = np.zeros((3, 3, 3, 3))
    for i in range(3):
        for j in range(3):
            if i==j:
                s_m = i
                ij_eq = True
            elif i+j == 3:
                s_m = 3
                ij_eq = False
            elif i+j == 2:
                s_m = 4
                ij_eq = False
            elif i+j == 1:
                s_m = 5
                ij_eq = False
            for k in range(3):
                for l in range(3):
                    if k==l:
                        s_n = k
                        kl_eq = True
                    elif k+l == 3:
                        s_n = 3
                        kl_eq = False
                    elif k+l == 2:
                        s_n = 4
                        kl_eq = False
                    elif k+l == 1:
                        s_n = 5
                        kl_eq = False
                    if ij_eq and kl_eq:
                        S_ijkl[i, j, k, l] = dat_s[s_m, s_n]
                    elif not ij_eq and not kl_eq:
                        S_ijkl[i, j, k, l] = dat_s[s_m, s_n]/4.0
                    else:
                        S_ijkl[i, j, k, l] = dat_s[s_m, s_n]/2.0
    return S_ijkl


S_ijkl = tranS_ijkl(dat_s)
sample_count = 500       ### 网格数量

### 在空间球面上均匀采样
v_theta = np.linspace(0, np.pi, sample_count)
v_phi = np.linspace(0, 2.0*np.pi, sample_count)
V_theta, V_phi = np.meshgrid(v_theta, v_phi)
a_x = np.sin(V_theta)*np.cos(V_phi)
a_y = np.sin(V_theta)*np.sin(V_phi)
a_z = np.cos(V_theta)
v_A = [a_x, a_y, a_z]

E_a_1 = np.zeros((sample_count, sample_count))
for i in range(3):
    for j in range(3):
        for k in range(3):
            for l in range(3):
                E_a_1 = E_a_1 + v_A[i]*v_A[j]*v_A[k]*v_A[l]*S_ijkl[i, j, k, l]

E_a = 1.0/E_a_1     ### 取倒数得到杨氏模量，单位为GPa
plt.figure(dpi=200)
ax = plt.subplot(111, projection='3d')
ax.set_xlabel('Ex')
ax.set_ylabel('Ey') 
ax.set_zlabel('Ez') 
ax.set_title("Young's Modulus(GPa)")
ax.__eq__ = True
ax.plot_surface(E_a*a_x, E_a*a_y, E_a*a_z, rstride=1, cstride=1, color='y')
plt.savefig('young3D.jpg')
plt.show()

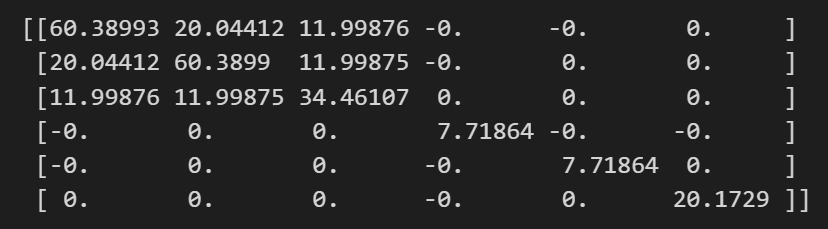
这是计算得到的弹性矩阵：

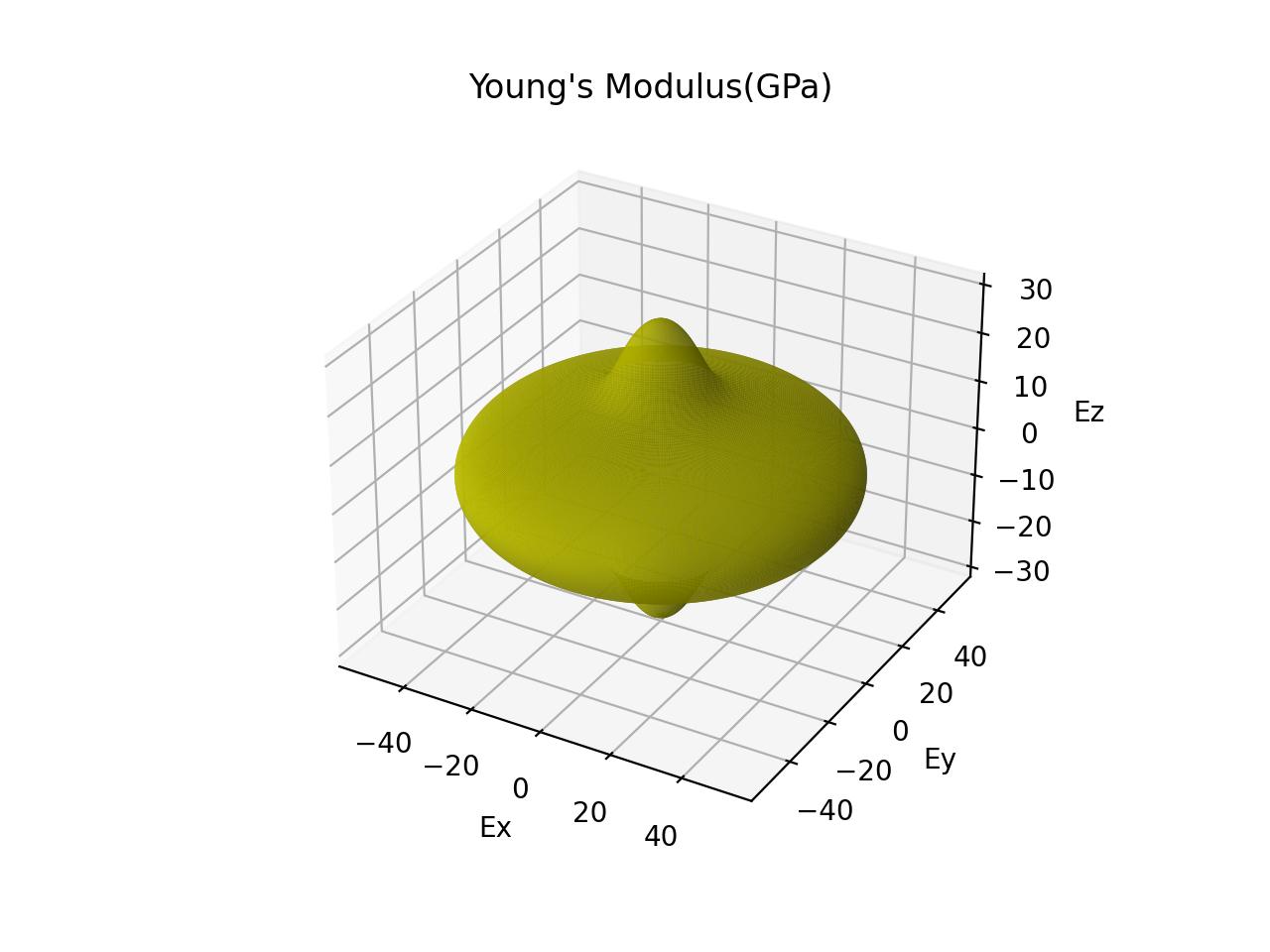
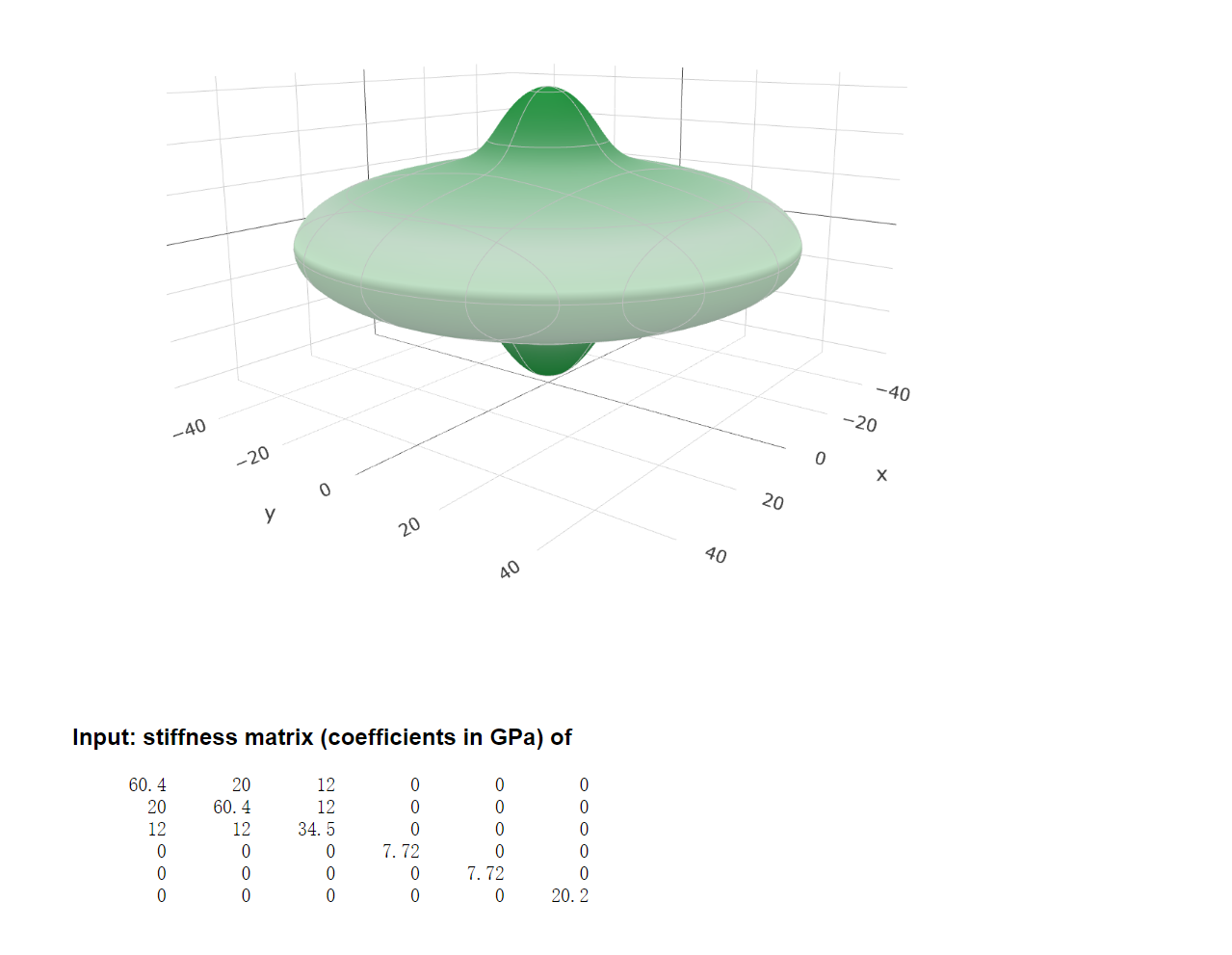
这是给出的空间角度分布杨氏模量：

将计算得到的弹性矩阵输入到 ELATE 中能得到相同的结果，证明了结果的正确性：

2.Python计算2D材料的角度分布杨氏模量和泊松比，以及画图

计算二维材料时需要注意的是由于二维材料的弹性矩阵的单位是N/m，因此需要将vasp计算得到的弹性矩阵预处理一下。下面是代码：

import numpy as np
import os
import pandas as pd
import matplotlib.pyplot as plt


### 读取弹性矩阵
os.system('grep -A 8 "TOTAL ELASTIC" OUTCAR | tail -6 > ecs.dat')
str_c = os.popen("grep -A 3 'lattice vectors' OUTCAR | tail -1 | awk '{print $3}'")
lat_c = float(str_c[0])
# lat_c = 16.0
df_ecs = pd.read_csv('ecs.dat', header=None, index_col=0, delimiter=r"\s+")
dat_ecs = df_ecs.values       ### 得到弹性矩阵


### 将vasp给出的弹性矩阵转换成满足Voigt下标的矩阵形式并将单位转换为GPa
dat_c = np.zeros(dat_ecs.shape)
for m in range(6):
    if m <= 2:
        m_ = m
    elif m == 3 or m == 4:
        m_ = m + 1
    elif m == 5:
        m_ = 3
    for n in range(6):
        if n <= 2:
            n_ = n
        elif n == 3 or n == 4:
            n_ = n + 1
        elif n == 5:
            n_ = 3
        dat_c[m, n] = dat_ecs[m_, n_]*0.01*lat_c
# print(dat_c)

################################### 改动部分 ########################################
dat_c = np.zeros((6, 6))                                                           #      
dat_c[0, 0] = 105.2                                                                #  
dat_c[0, 1] = 18.4                                                                 # 
dat_c[1, 0] = dat_c[0, 1]                                                          #        
dat_c[1, 1] = 26.2                                                                 # 
dat_c[2, 2] = 1.0                                                                  #
dat_c[3, 3] = 1.0                                                                  #
dat_c[4, 4] = 1.0                                                                  #
dat_c[5, 5] = 22.4                                                                 # 
################################### 改动部分 ########################################

### 计算柔度矩阵
dat_s = np.linalg.inv(dat_c)       

### 将二维柔度矩阵转换成四维柔度矩阵
def tranS_ijkl(dat_s):
    '''
    将6x6的二维柔度矩阵转换成2x2x2x2的柔度矩阵
    '''
    S_ijkl = np.zeros((2, 2, 2, 2))
    for i in range(2):
        for j in range(2):
            if i==j:
                s_m = i
                ij_eq = True
            elif i+j == 1:
                s_m = 5
                ij_eq = False
            for k in range(2):
                for l in range(2):
                    if k==l:
                        s_n = k
                        kl_eq = True
                    elif k+l == 1:
                        s_n = 5
                        kl_eq = False
                    
                    if ij_eq and kl_eq:
                        S_ijkl[i, j, k, l] = dat_s[s_m, s_n]
                    elif not ij_eq and not kl_eq:
                        S_ijkl[i, j, k, l] = dat_s[s_m, s_n]/4.0
                    else:
                        S_ijkl[i, j, k, l] = dat_s[s_m, s_n]/2.0
    return S_ijkl


S_ijkl = tranS_ijkl(dat_s)
sample_count = 1000       ### 网格数量

### 在空间球面上均匀采样
v_phi = np.linspace(0, 2.0*np.pi, sample_count)
a_x = np.cos(v_phi)
a_y = np.sin(v_phi)

v_A = [a_x, a_y]
v_B = [-1.0*a_y, a_x]

E_a_1 = np.zeros(sample_count)
v_ab_1 = np.zeros(sample_count)
for i in range(2):
    for j in range(2):
        for k in range(2):
            for l in range(2):
                E_a_1 = E_a_1 + v_A[i]*v_A[j]*v_A[k]*v_A[l]*S_ijkl[i, j, k, l]
                v_ab_1 = v_ab_1 + v_A[i]*v_A[j]*v_B[k]*v_B[l]*S_ijkl[i, j, k, l]


E_a = 1.0/E_a_1     ### 取倒数得到杨氏模量，单位从为GPa
v_ab = -1.0*v_ab_1/E_a_1


plt.figure(dpi=200)
ax_E = plt.subplot(121, projection='polar')
ax_E.set_title("Young's Modulus(N/m)")
ax_E.plot(v_phi,E_a,'-',lw=1.5,color='r')
ax_E.fill(v_phi,E_a,'r',alpha=0.2)
ax_E.set_rgrids(np.arange(0, 1.2*np.max(E_a), 20))

ax_v = plt.subplot(122, projection='polar')
ax_v.set_title("Poisson's Ratio")
ax_v.plot(v_phi,v_ab,'-',lw=1.5,color='g')
ax_v.fill(v_phi,v_ab,'g',alpha=0.2)
ax_v.set_rgrids(np.arange(0, 1.2*np.max(v_ab), 0.1))
plt.savefig('young2D.jpg')
plt.show()

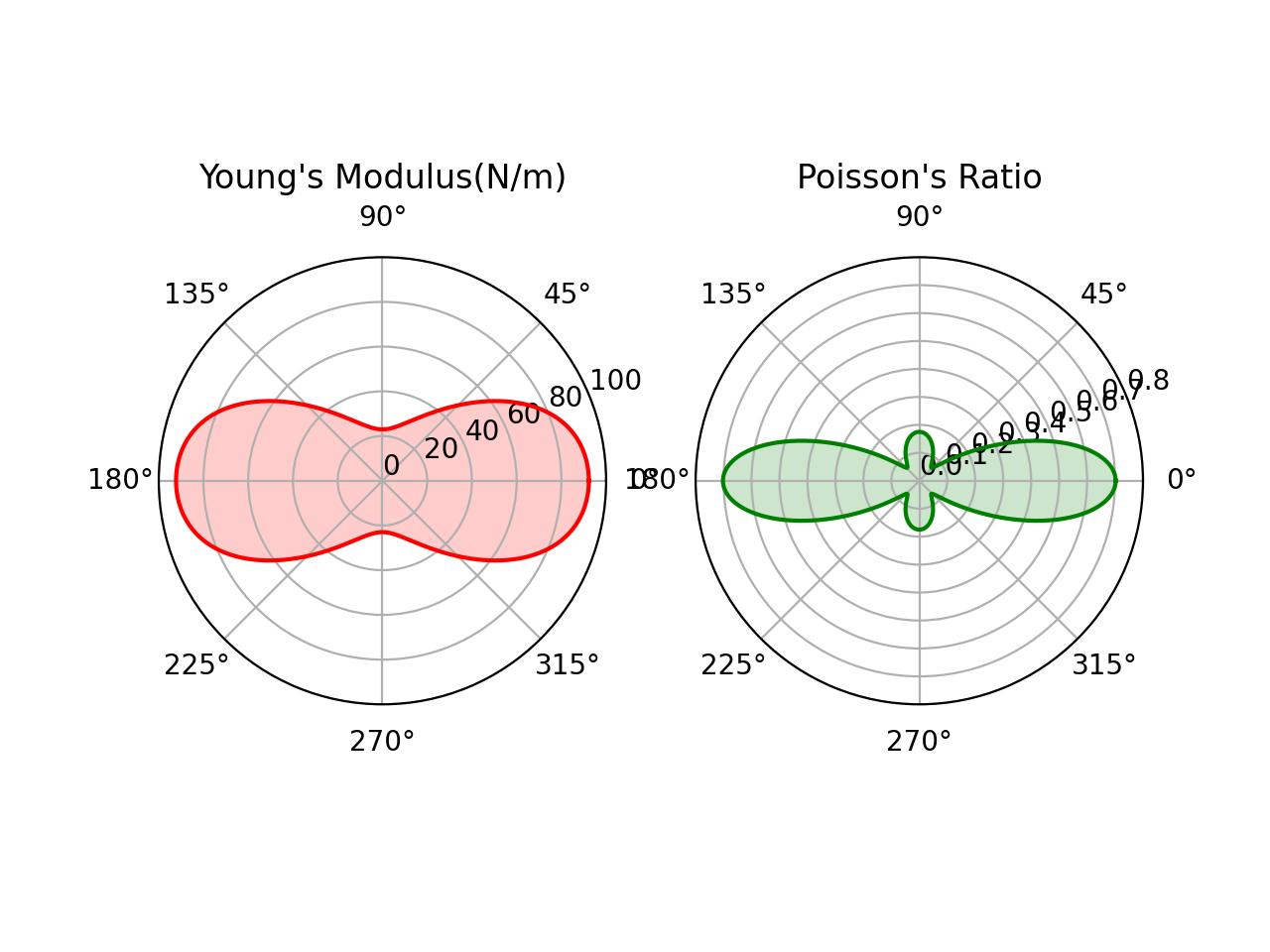
画图部分参考了这篇文章的画图方法：https://www.sohu.com/a/445105422_816426。同时为了验证计算结果的准确性，使用了文章中的弹性数据来计算，具体见上面代码的 ###改动部分###,以下为运行后得到的结果：

与文章中结果一致，证明了计算的正确性。