vasp+phonopy计算声子谱
一、从薛定谔方程到声子
在开始计算声子谱之前,我们首先需要搞清楚什么是声子,不同于电子、中子、质子等实体粒子,声子不是一种实体粒子,而是一种描述晶格振动模式的量子化的准粒子。它完全是人们为了描述晶格振动而引入的一种理论模型,并没有任何实际物体对应,这一点并不难理解,就像超弦理论并没有弦一样…但是要理解声子的由来还是需要花费一点功夫的,这里我们可以先从单粒子的薛定谔方程说起。
1.一维无限深方势阱的单粒子的定态薛定谔方程
对于长度为a的一维势阱中的自由单粒子,其薛定谔方程形式满足:
定态条件下,不考虑波函数随时间的演化,因此波函数化为:
上式为常系数二阶微分方程,其解的形式为
可以看到波函数有正弦波的形式,另外也可以写成指数的形式,即,同时,在势阱壁上还需要满足边界条件,即:
将以上边界条件带入波函数中,可以求得:
即是, 有:
由此可以得到以下结论:
- 粒子的能级是分立不连续的;
- 粒子的运动模式有多种,即波函数的形式不固定,存在多种,每一种对应不同的本征能量。
2.从单粒子到多粒子
以上描述的单粒子的情况,如果这一体系中存在多个相同的粒子呢?此时我们只需要在薛定谔方程上加一个指标就可以了,即是:
当然这么做的前提是完全忽略粒子之间的相互作用。可以看到,对于任何粒子,以上关于这一关系都满足,因此每个粒子所有的运动模式是相同的,并且都对应相同的本征能量,这一式子也被称作本征方程。最后体系的总的能量和总的波函数一定可以分解为这些粒子单个波函数的线性叠加,即是:
如果认为k的取值是连续的,那么E-k能量色散曲线是抛物线的形式,如下图:
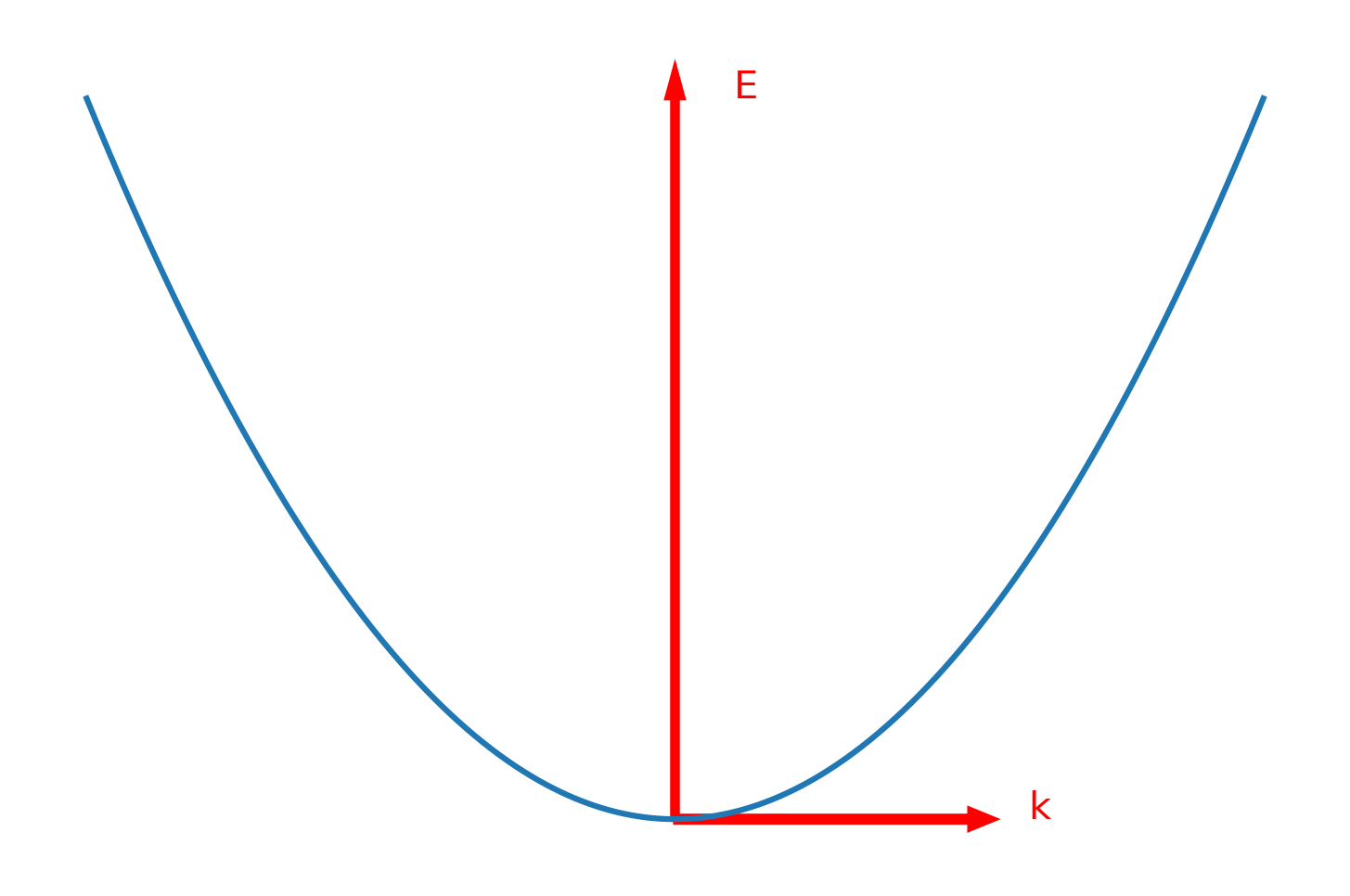
3.一维单原子链
在简谐近似下,根据牛顿运动定律,单原子链中第n个原子的振动方程满足:
该方程形式上和上面类似,同样是二阶线性微分方程,因此其解也应有正弦波的形式,假设方程的解有格波的形式,即:
和1中的一样,我们将形式解带入上面的振动方程中,可以得到:
这表明和k之间存在一定的色散关系,进一步,再引入周期性的边界条件,可以得出是关于k的周期性函数,把k的取值仅限定在一个周期内,即是-,那么与k之间的色散曲线如下图:
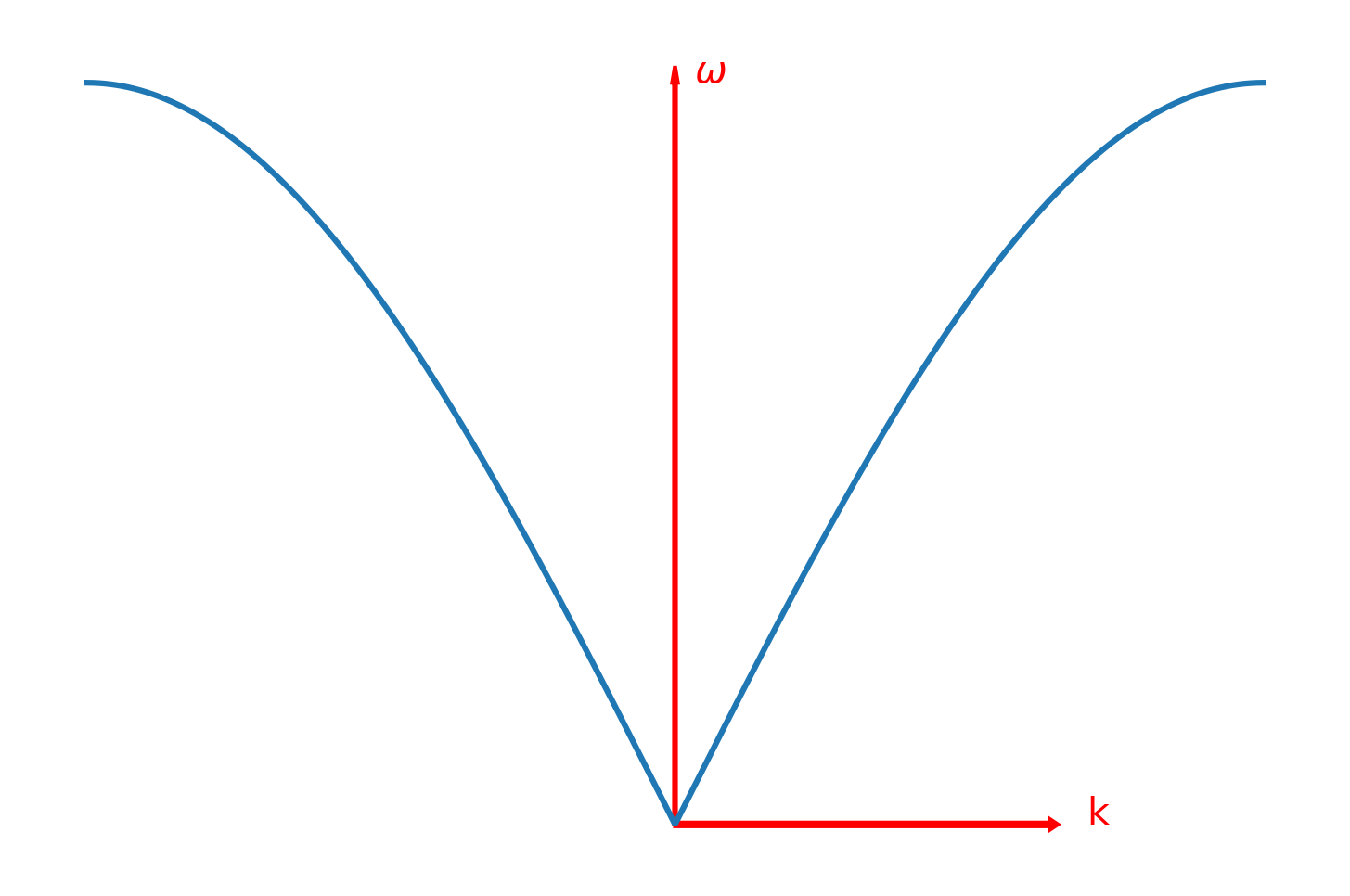
这是一个格点振动的情况,对于其它多格点,与上面一样,由于这是一个本征方程,所有的格点都满足这个方程,所以所有格点的振动模式都符合这一振动模式,单原子链总的振动模式可以有这些单原子的振动模式叠加获得。
4.引入声子
到了这里就可以很自然地引入声子。前面1、2节中为了描述一维方势阱中粒子的能级,我们求解了定态薛定谔方程,最后得出粒子的能级不是连续的,而是分立的,一份一份的,并且存在最小能量,对于这样一种体系,我们可以认为存在一种能量子,这一体系的能量只能是这一能量子的整数倍,于是在描述一维原子链中原子的振动模式,引入了简正坐标之后,可以得到体系的总能量为:
可以看到体系的总能量同样是量子化的,并且是以为激发单元,因此很自然这里我们引入了声子,用声子来描述体系能量激发的最小单元。
5.关于声子的一些知识
- 声子谱:声子频率与波矢k之间的色散关系(布里渊区之内)
- 光学支:k->0时,->!0
- 声学支:k->0时,->0
- 对于m维晶体,原胞内有n个原子,那么原胞内原子的振动自由度为mn,有m支声学波,m(n-1)支光学波
二、vasp+phonopy计算Si的声子谱
1. 关于声子谱的一个常识
通过声子谱我们可以看出材料的热力学稳定性,当声子谱全部在0点以上时,说明材料没有出现虚频,即材料是相对稳定的。
计算声子谱的方法主要有两种,分别是有限位移法和密度泛函微扰理论,首先介绍第一种方法:
2. 有限位移法
2.1 对原胞进行高精度的结构优化
主要影响的参数:EDIFF, EDIFFG, ISIF
优化之后得到优化的结构CONTCAR.
2.2 将原胞阔胞并获得有位移的结构
输入以下命令(phonopy已经安装好):
1 | phonopy -d --dim='3 3 3' -c CONTCAR |
运行后如下图:
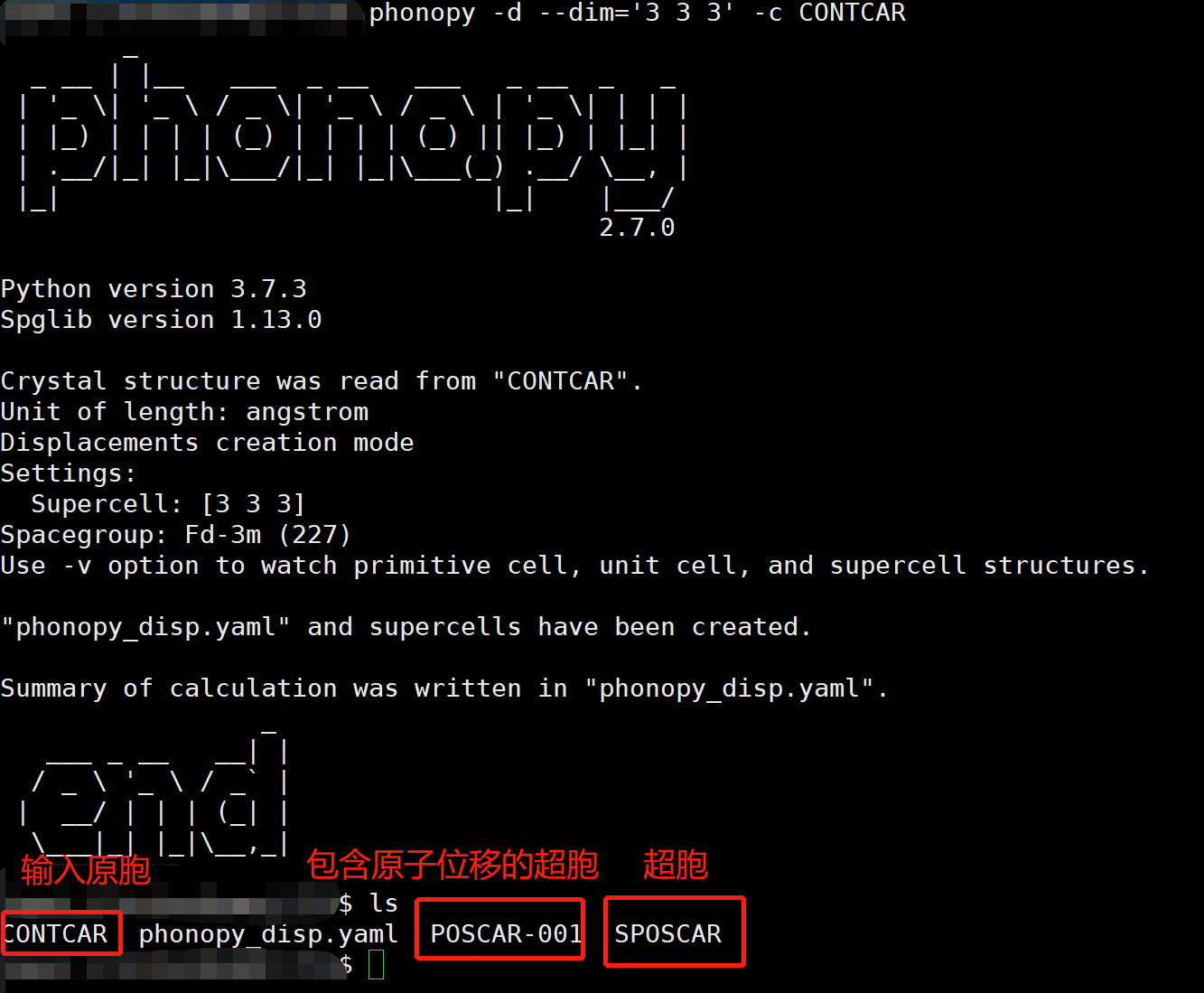
其中POSCAR-001就是我们需要的包含原子位移的超胞,值得一提的是,由于这里我们使用的单晶硅的结构较为简单,因此只生成了一个位移文件,当结构较为复杂时,可能有多个文件,这些文件在后面都需要计算。
2.3 用位移超胞做单点计算
- INCAR设置中需要注意的地方:单点计算,因此NSW=0,并且需要计算Hellmann−Feynman力,ISIF不能设置为0
- 由于扩胞了,注意减小KPOINTS中网格密度
2.4 提取原子受到的Hellmann−Feynman力
1 | phonopy -f disp-001/vasprun.xml |
运行后如下:
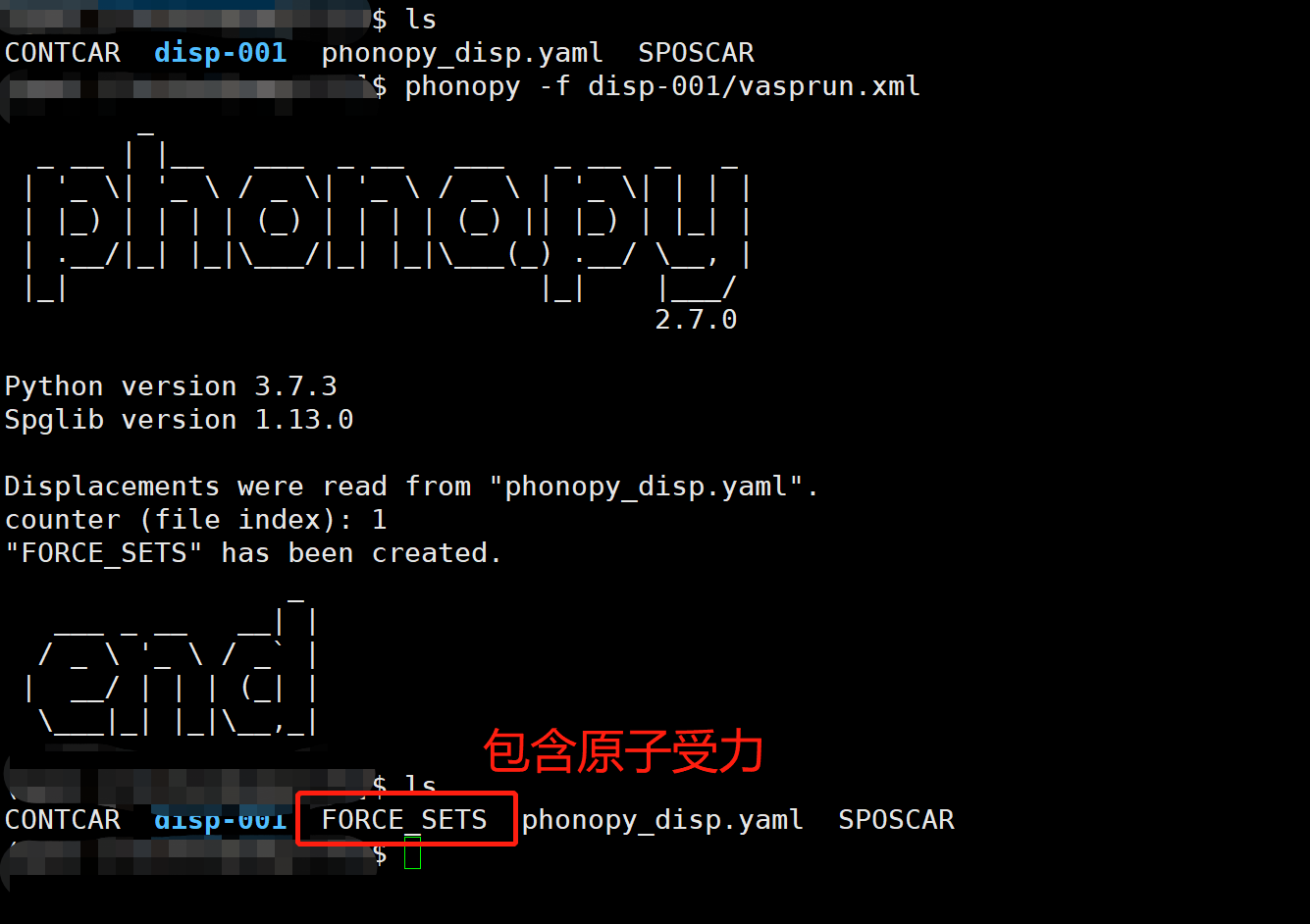
其中 FORCE_SETS 就是我们需要文件。
2.5 数据处理,提取声子谱
首先需要准备band.conf配置文件,配置文件中的参数可以参考官网说明:https://phonopy.github.io/phonopy/setting-tags.html
我的band.conf文件内容如下:
1 | ATOM_NAME = Si |
准备好band.conf文件后,运行
1 | phonopy -p -s band.conf |
即可得到.pdf的声子谱文件,如下:
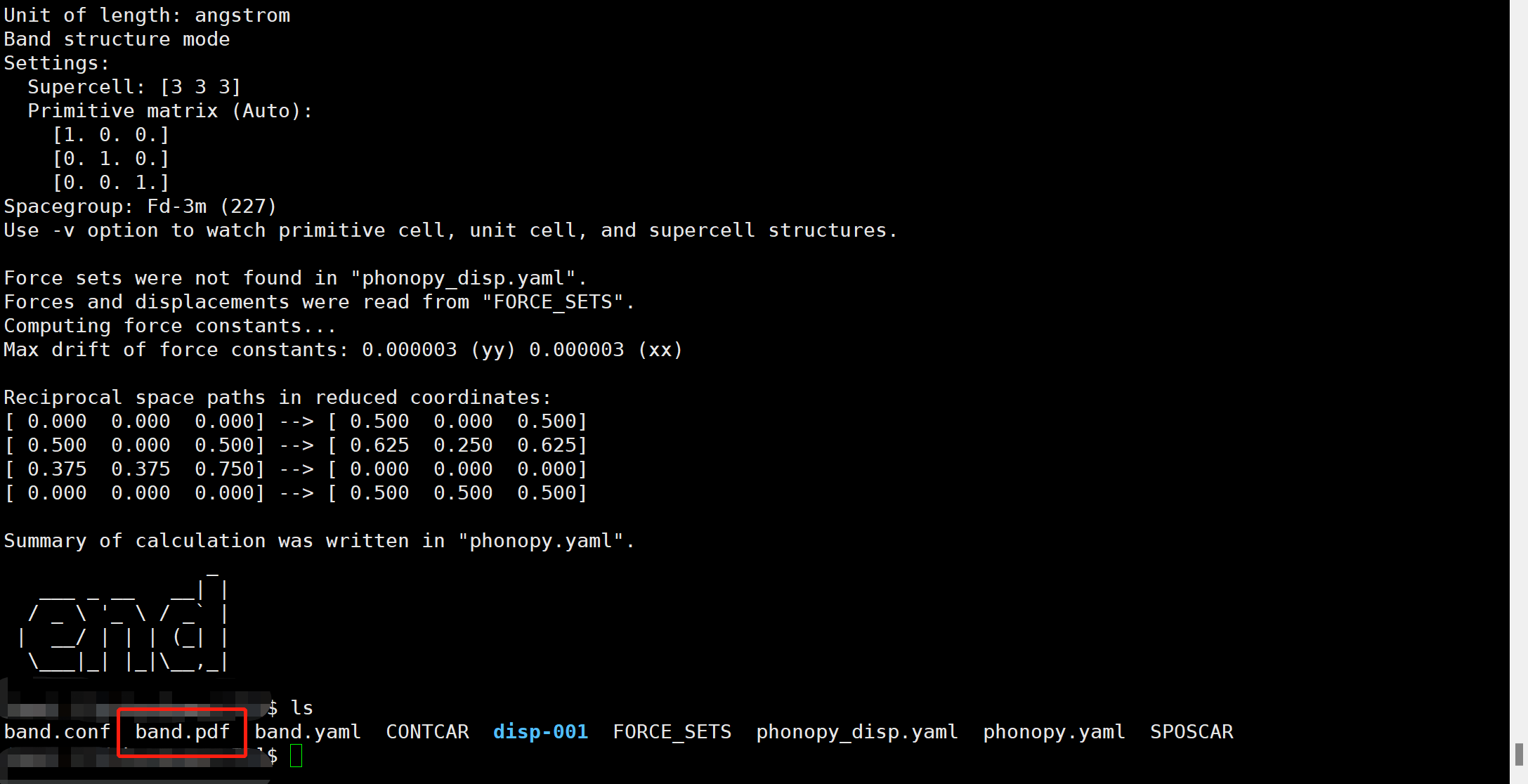
如下是计算得到的声子谱:
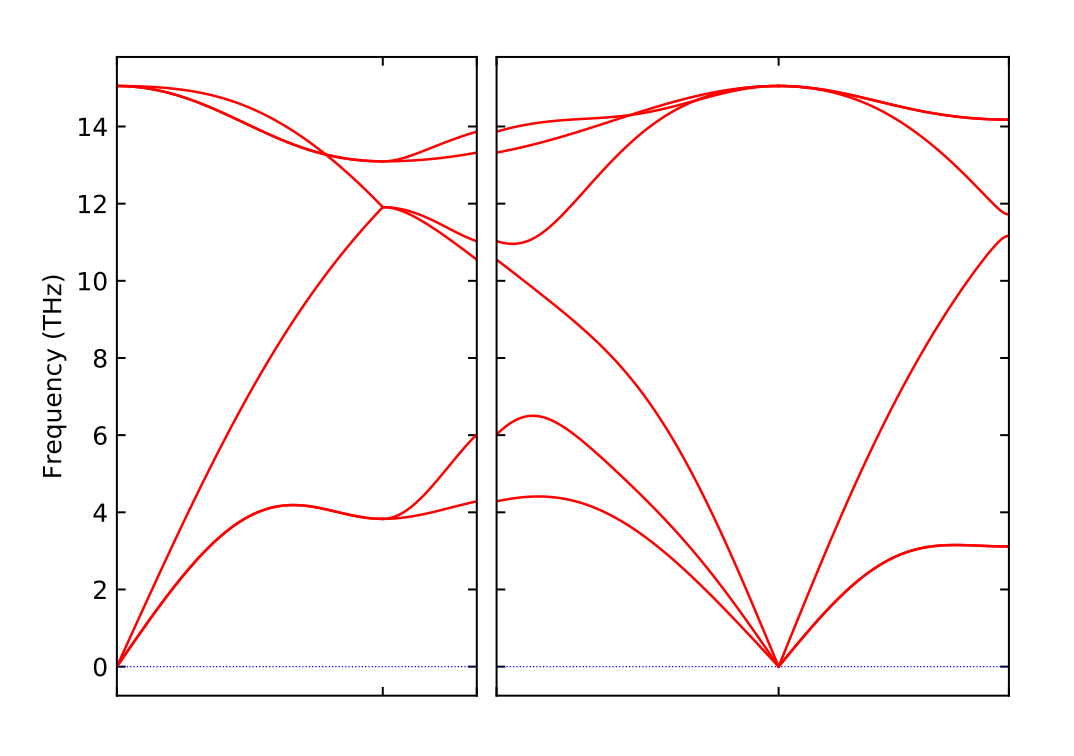
3. 密度泛函微扰理论
3.1 对原胞进行高精度结构优化
这一步与上一方法中相同,省略。
3.2 构建超胞
严格来说这一步与上一方法中略有不同,这里不需要有位移超胞,而是只需要初始超胞,但是由于上一方法中同样可以产生完美的超胞,因此使用的命令与上一方法中相同,最后需要使用的 SPOSCAR 文件。
3.3 使用vasp进行微扰计算
- 这一步中 INCAR 文件的参数需要调整,主要包括以下要点:
- NSW = 1
- IBRION = 8(微扰计算,声子计算专用)
- NPAR,NCORE,KPAR等并行参数都关闭,不然会报错
- 为了减小计算量,建议打开对称性开关 ISYM = 2
- 同样注意调整KPOINTS中k点的密度
3.4 计算力常数
直接输入命令:
1 | phonopy --fc calc-force/vasprun.xml |
得到的 FORCE_CONSTANTS 即为我们需要的文件,如下图:
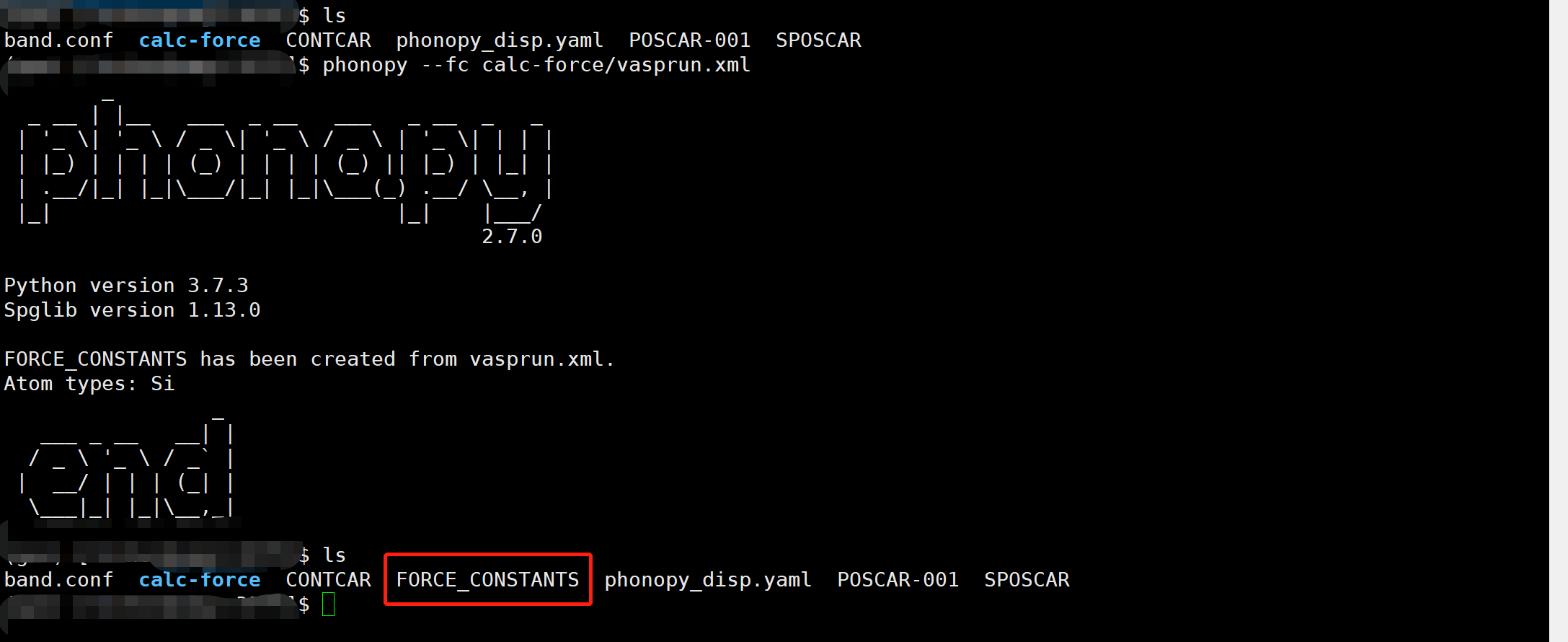
3.5 数据处理,提取声子谱
这一步与上一方法中该步也相同,首先需要准备band.conf文件,内容如下:
1 | ATOM_NAME = Si |
其中增加的参数 FORCE_CONSTANTS 表示从力常数读取数据。
最后输入命令:
1 | phonopy -p -s band.conf |
即可得到声子谱文件,和上一方法类似,就可以得到声子谱图,如下:
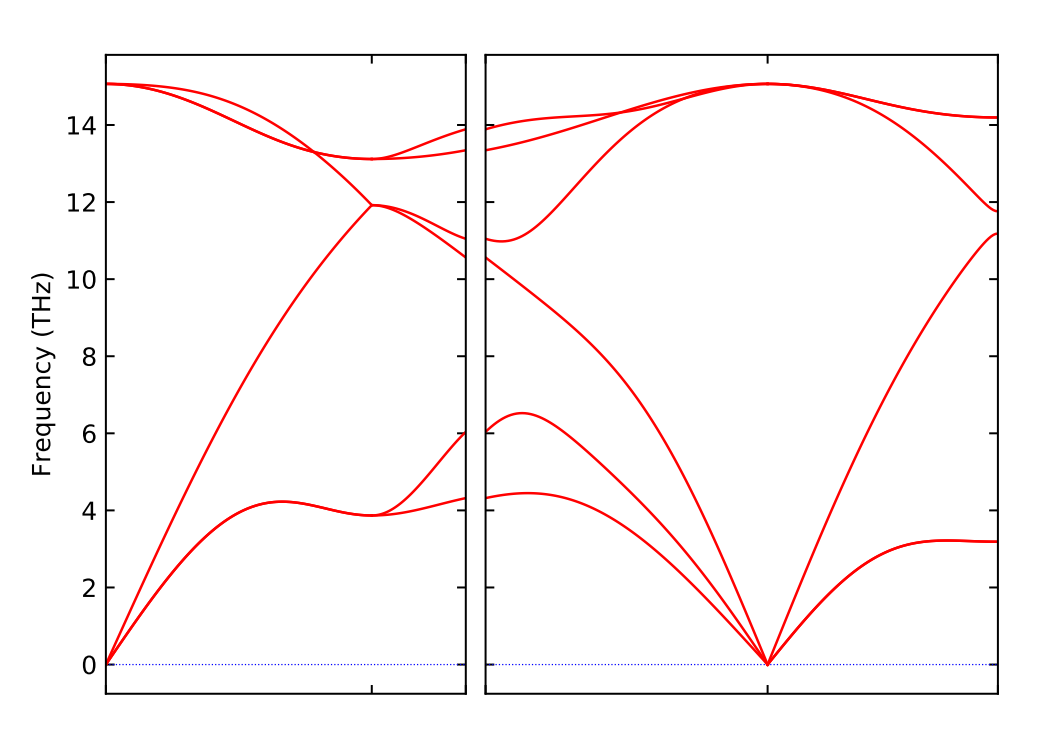
三、参考资料
[1]. 量子力学(卷1).曾谨言著.
[2]. 固体物理.黄昆著.
[3]. 有限位移法
[4]. 密度泛函微扰理论
[5]. phonopy官网